Rollbahnen für Kugeln sind ein wichtiges Instrumentarium der Hands-on- Physik.
Welche Bahn wird eine Kugel nehmen, wenn ich sie von einer kleinen Rampe aus hinein rollen lasse?
Das hängt natürlich ab von der Bodenform der Unterlage – und davon, wie viel Schwung ich ihr mitgebe.

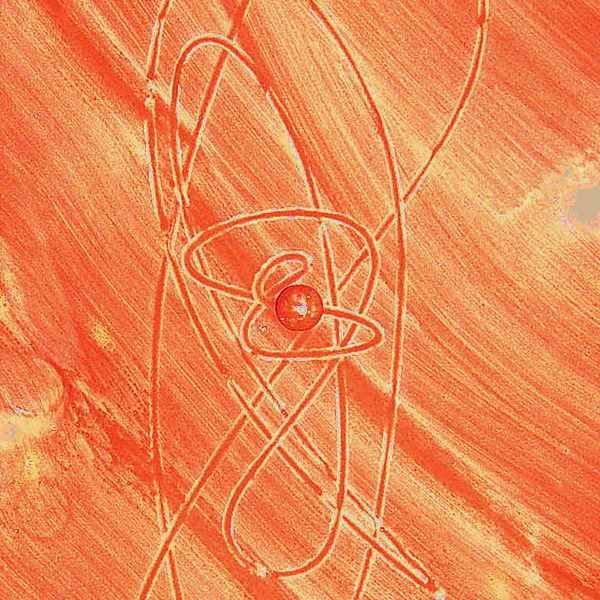
Im Fall der Station SCHIEFE BAHN ist der Boden eben; eine schwarze Platte, die mit unterschiedlicher Neigung aufgestellt werden kann. Sie wird mit Schwamm und etwas Kreidepulver eingestrichen, sodass sich die Bahnen der Kugeln einzeichnen.
Im obigen Bild ist die Platte leicht schräg gestellt. Die Bahnlinie wird durch die Schwerkraft gekrümmt und biegt sich zu einer eleganten geometrischen Figur.
Dieses einfache Setting erlaubt es, die unterschiedlichsten Szenarien durchzuspielen:
Auf waagrecht gestellter Platte wird die Kugelbahn zum geradlinigen Strich.
Stossen zwei Kugeln zusammen, so reflektieren sie einander, die Striche erhalten einen Knick.

Ähnlich beim Stoss an die Wand.
Wie sieht es aus, wenn zwei unterschiedliche Kugeln zusammen stossen?
Lassen sich vielleicht alle Bahnen der Körper mathematisch erfassen und beschreiben? Gerade Linien, messbare Winkel, Kreise, Parabeln, Elypsen … ?
Dies wurde zum Programm der neuzeitlichen Physik, die vor etwa vierhundert Jahren mit Galilei und Descartes ihren Anfang nahm: Die Bewegungen der Objekte lassen sich exakt erfassen, wenn man die Kräfte dingfest macht, durch welche sie angetrieben werden.
Das Zusammenspiel der Kräfte kann als mathematische Gleichung aufgestellt werden. Und löst man diese Gleichung, dann kann man im Vorhinein schon sagen, wie sich das Objekt nachher bewegen wird.

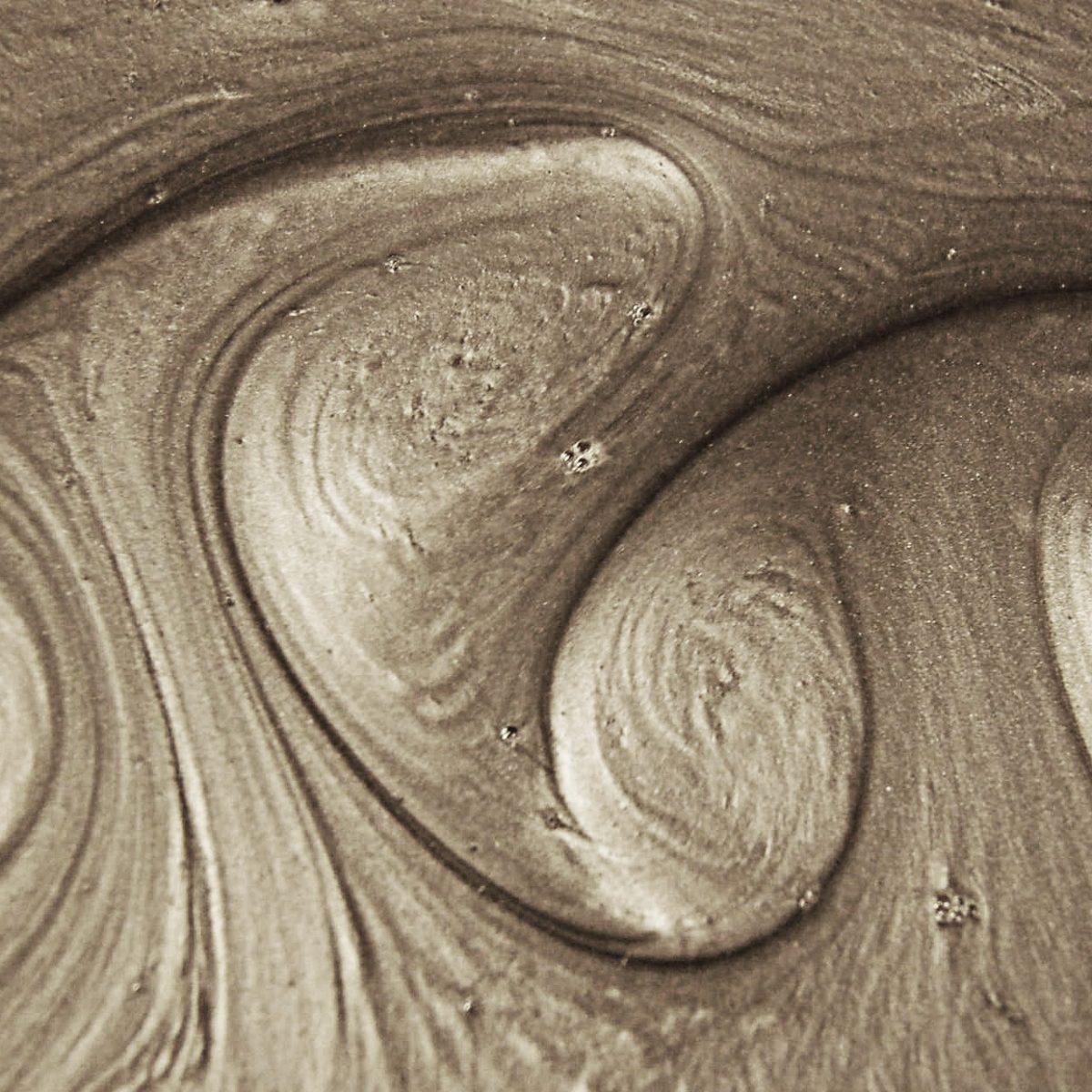
Bei der Station POTENTIALTOPF ist die Bodenform schüsselförmig. Lasse ich hier ein Kugel hineinrollen, dann krümmt sich die Bahnlinie zu Kreisen und Elypsen.
Es eröffnet sich ein variantenreiches Spiel der Formen – je nachdem, wo, unter welchem Winkel und mit welcher Geschwindigkeit ich die Kugel hinein rolle.

In der Station POTENTIALLANDSCHAFT wird schließlich das Thema noch weiter geführt – die Bodenform wird zu einer beliebig gestaltbaren „Landschaft“ erweitert.
Welche Bahn wird die Kugel jetzt nehmen?
Und umgekehrt: Wie muss ich die „Landschaft“ modellieren, damit eine bestimmte Bahnkurve herauskommt?